Sia U la moneta in vigore. Un'industria produce due prodotti X e Y e con due macchinari P e Q. Per ogni unità di X sono necessarie 1 ora di P e 3 ore di Q, per ogni unità di Y servono 2 ore di P e 2 ore di Q. Inoltre X non può essere prodotto in più di 18 pezzi settimanali, la macchina P non può lavorare per più di 40 ore alla settimana, mentre B per non più di 60. Qual è la combinazione produttiva per cui il ricavo Z è massimo se ogni unità di X viene venduta a 16000 U e ogni unità di Y a 10000 U? modello matematico:  massimizzare z = 16 mila x + 10 mila y  se x+2y≤40, 3x+2y≤60, 0≤x≤18, 0≤y
 

Tracciamo il poligono che rappresenta le quantità di X e di Y ammissibili e poi determiniamo le quantità di X e di Y per cui il ricavo (16 000 X + 10 000 Y) è massimo. 16 000 X + 10 000 Y = 318 000 quando  X = 18, Y = 3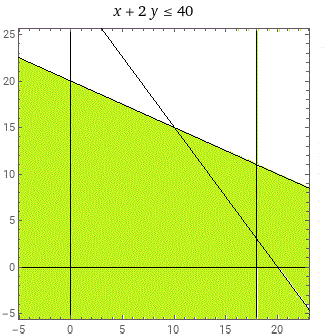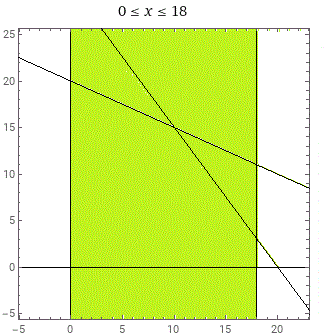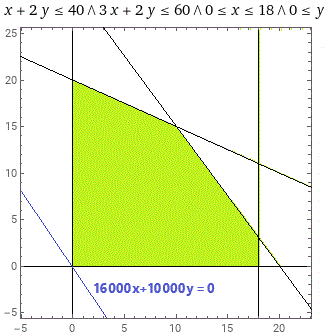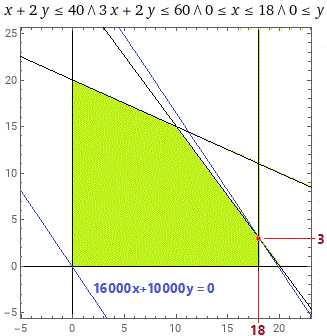

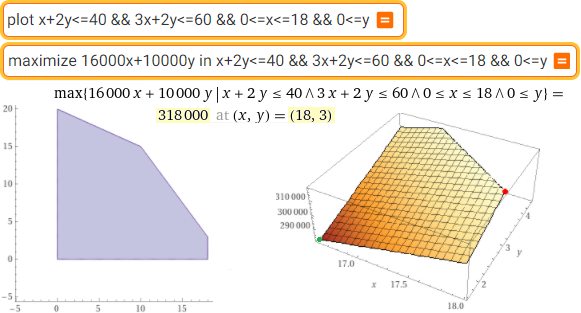
Si può risolvere il problema facilmente con WolframAlpha:


plot x+2y<=40 && 3x+2y<=60 && 0<=x<=18 && 0<=y
maximize 16000x+10000y in x+2y<=40 && 3x+2y<=60 && 0<=x<=18 && 0<=y